Quiz : Time Required to Heat Water

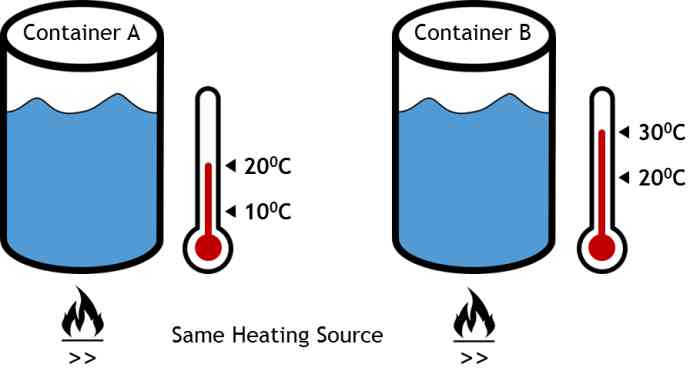
This quiz is about heating time required to increase the temperature of water. Imagine that there are two containers filled with same mass of water. The initial temperature of water in Container A is 100C and that in Container B is 200C.

To simplify the problem, imagine that both the containers are insulated with perfect insulation, mean there is zero heat loss in the atmosphere during heating process. Both the containers are identical in all the aspects including shape, size, and material. The only difference is initial temperature of water insider the container.

 Quiz-Heating-Time-For-Water-Initial-Tempeature

Water in both the containers is heated with same heat source. It means, the rate of heat addition in both the containers is same. Water in container A is to be heated from 100C to 200C. Water in container B is to be heated from 200C to 300C. 

Quiz-Heating-Time-For-Water-Initial-delta-T

Question

With above conditions, answer the following question:

To increase the temperature of water (100C to 200C for container A, and 200C to 300C for container B), time required for heating will be

  1. Same for both the containers
  2. Container A will take more time than container B
  3. Container B will take more time than container A
  4. Insufficient data provided. Cannot be predicted.

 

How to post your answer ?

Post your answer as a comment at the bottom of this page. Login to your LearnCAx account or write your Name and Email ID so that we can publish the answer. Make sure to check “Notify me of follow-up comments” to receive notification about all the updates on this quiz.

Write your choice of answer from above four options. It is also expected (but not compulsory) that you should write the reason (or justification) for your answer. All the answers will be published on 18th September 2014. We will also post the correct answer with a justification.

 

Earn Reward Points

  1. Earn 1 point only for the correct choice without justification
  2. Earn 3 points for correct choice with justification
  3. Earn 5 points if you answer is selected as one of the best answer
  4. After looking at few answers, I am forced to add this. A correct choice which wrong justification will get 0 points☺

These reward points could be used to get discount on all our courses and projects.

 

Quiz Participation

Thanks for participating in the quiz. Looks like there are total 800 people seen this quiz (Rough data based on number of visitors). Out of 800 people, 13 people have answered the quiz. Congratulations to those who have answered the question. You already fall into elite group of 1.6 % people answering the question.

Following the analysis of answers given:

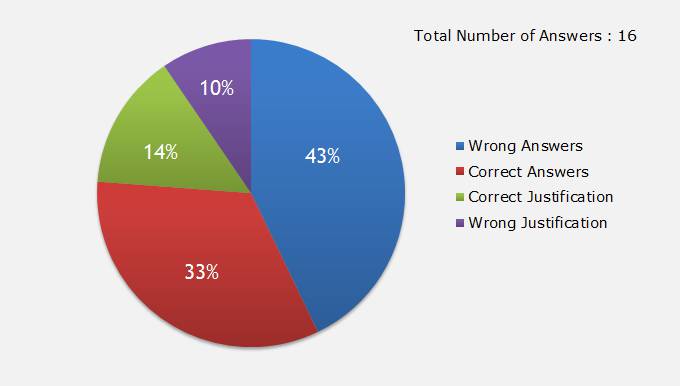
partipant-analysis

Total 13 reward points are given by LearnCAx to various participants. Those who have answered will receive a separate email notification about the reward points earned.

Best answer

The best answer selected is given by “Bruno”. Bruno writes:

“Container A will take more time then container B.
The time would only be the same if we could consider that the enthalpy variation was linear, which it isn't (although it almost is). But the enthalpy change from 20 to 30 C is slightly smaller than from 10 to 20, so heating container B from 20 to 30 should take a slightly smaller time.”

Read all the answers given in below comments. It was a great learning experience for us to read your answers. We are sure every visitor will also feel same.

Note: The reward points and best answer is selected by LearnCAx team after doing detailed analysis. By no means, we want to question anyone’s understanding about the physics. These quizzes are created just to share different views and have a fun!!

 

Answer by LearnCAx Team

The correct answer is

2: Container A will take more time than container B

Importance of assumptions

It is assumed that there is no heat loss from container to atmosphere. If we do not make this assumption, container B will have more heat loss as compared to container A. Without this assumption, this difference will play some role in deciding heating time.

It is assumed that rate of heat addition in both containers is same. Note that we are assuming the amount of heat addition is same. In case even if heat source is same, the rate of heat addition is decided by conductivity, viscosity (as this is natural convection). As we are assuming that rate of heat addition is same, mean no matter what happens inside the tank, the water inside tank is going to absorb the same amount of heat. So conductivity and viscosity is not playing any role in time required to increase the temperature.

Justification for our answer

With above assumptions true, the only factor deciding time required to increase the temperature is Cp (Specific Heat of Water). 

Heating time required:
= (Heat required for 100C temperature rise) / (Rate of heat addition)
= (m x Cp x ΔT) / (Rate of heat addition)

Where:

  • Rate of heat addition is same for both containers
  • m = Mass of water (Same for both containers)
  • ΔT = Temperature difference between initial and final temperature (100C for both containers)
  • Cp = Specific heat of water

As all the parameters are same, we need to check variation of Cp with respect to temperature.

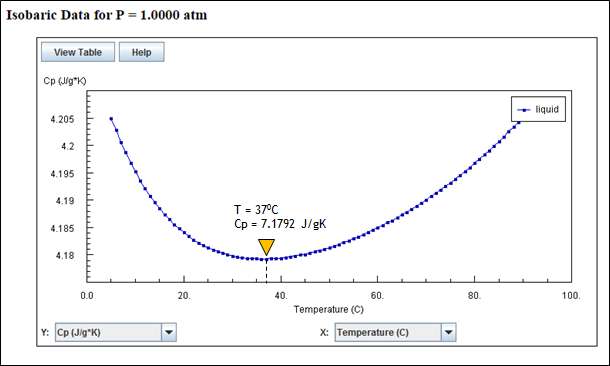
Cp variation with temperature is non-linear. If we see the variation of Cp from 50C to 900C, Cp is decreasing with temperature with minimum value at 370C and then increasing. Following plot shows that variation.

Water-Cp-vs-temp-at-1-atm-pressure 

Lets look at Cp variation between 100C to 200C (for container A) and 200C to 300C (for container B). 

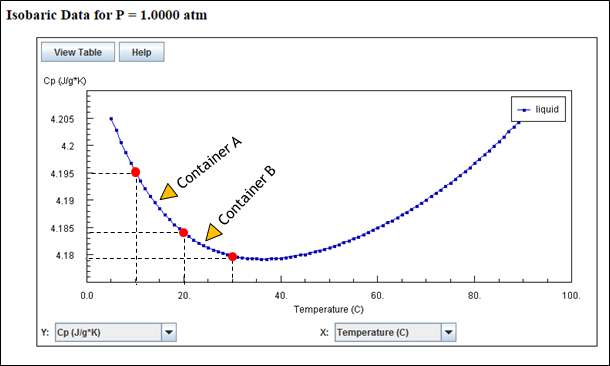
Water-Cp-vs-temp-at-1-atm-pressure-10-20-30-deg-c 

Above plot shows that Cp values for Container A temperature range (100C to 200C) is more that Cp values for Container B temperature range (200C to 300C). In order to estimate the actual heating time, we need to consider variation of Cp with respect to temperature (and hence with respect to time). So the calculations will be unsteady calculations. Even if we consider constant values (average of minimum and maximum), the average value Cp for container A is more than average value Cp for container B.

All above property variations are taken from National Institute of Standards and Technology. If you want to check property variation Click here. A text file containing property variations of water with respect to temperature is attached with this article. You can download that after logging with LearnCAx account.

Let’s do a sample calculation

Assume following values:

Heat addition rate = 3500 J/s (A typical heat addition rate of gas stove)
m = 1000 grams (Approximate weight of 1 litre water)
ΔT = 100C (Temperature difference for both containers)

Let’s calculate average value of Cp for Container A and Container B by using following chart:

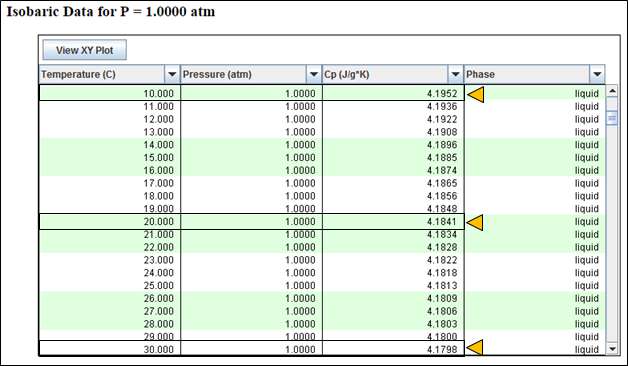
Water-Cp-vs-temp-at-1-atm-pressure-10-20-30-deg-c-chart

Average Cp value for Container A = (4.1952 + 4.1841) / 2 = 4.1896 J/gK

Average Cp value for Container B = (4.1841 + 4.1798)) / 2 = 4.1819 J/gK

Heating time for container can be calculated using following equation:

Heating time required:
= (Heat required for 100C temperature rise) / (Rate of heat addition)
= (m x Cp x ΔT) / (Rate of heat addition)

Heating time for container A:
= (1000 x 4.1896 x 10) / (3500)
= 11.97 Seconds

Heating time for container B:
= (1000 x 4.1819 x 10) / (3500)
= 11.95 Seconds

So heating time for Container A is more than that of Container B (although this might not be signification for you ☺).

Important Note: Above results are valid only with the assumptions made. You may see some different results in reality. In reality when you heat water, the container is not perfectly insulated. So the heat loss rate will increase with increase in temperature. Viscosity and conductivity of water decrease with temperature and will have some impact on heating time.

Hope you enjoyed the quiz. A PDF copy of this quiz with answer is available for download. Login with your LearnCAx account or Create Account to access the download section given at top.

 

The Author

{module [311]}